1. 우리는 미분의 이론적 배경을 배웠다.
- 1) 적분에서 유도한 미분의 정의($lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$),
- 2) 왜 미분이 기울기를 의미하는지 ($y = wx \to \frac{y}{x} = w$)
- 3) 속력은 거리의 미분이라는 것 ($s = vt \to \frac{s}{t} = v$)
- 4) $dx$가 무엇인지 (not zero, but almost zero)
- 5) $dx\to0$으로 갈때, 도함수는 접선의 기울기를 표현하는 함수가 됨.
- 6) "순간"의 "변화율"이라는 도함수의 역설 (순간은 시간이 없는것, 변화는 시간에 따라 변한것)
- 그런데 이것만 가지고는 부족하다. 실제로 계산하는법을 모르기 때문이다.
2. 다항함수의 미분법을 기하학으로 표현해보자 ($x^2$)
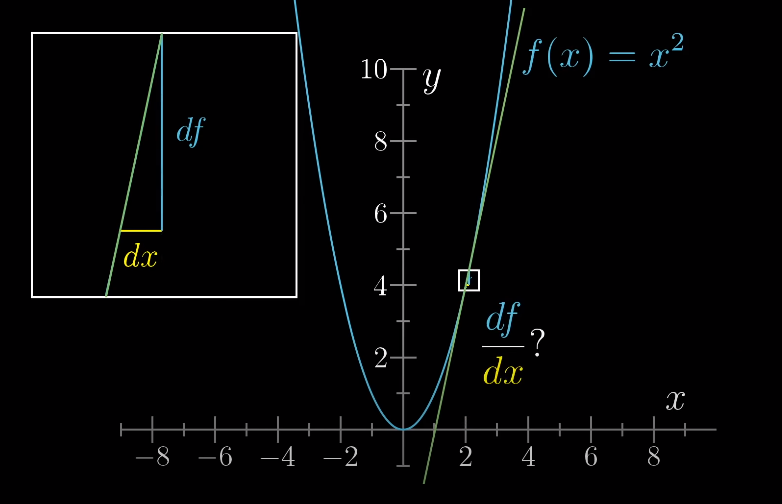[그림] $y = x^2$그래프
- 가장 쉬운 함수인 $y = x^2$에서 시작해보자. 우리는 $\frac{df}{dx}$가 미분계수라는 걸 알고 있다. (단, $dx\to0$)
- 그러나 그래프로 봐서는 실제로 크기를 가늠하기 어렵다. 대충 생각해서 숫자를 대입해서 한번 풀어보자.
- 만약 $x=2, y=4$인 지점에서 $x=2.01, y=4.0401$로 이동했다고 해보자.
- 그러면 $\frac{df}{dx} = \frac{0.401}{0.1} = 4 = 2x$이다. 정확히 4는 아니고 약 4정도 된다.
- 미분계수(도합수의 결과)는 어쨋든 근사치이기 때문에, $dx$가 더 작으면 에러가 더 줄어들 것이다.
- 그런데 사실 생각해보면 $x^2$은 저렇게 그래프처럼 그릴 수도 있지만, 정사각형으로도 그릴 수 있다.
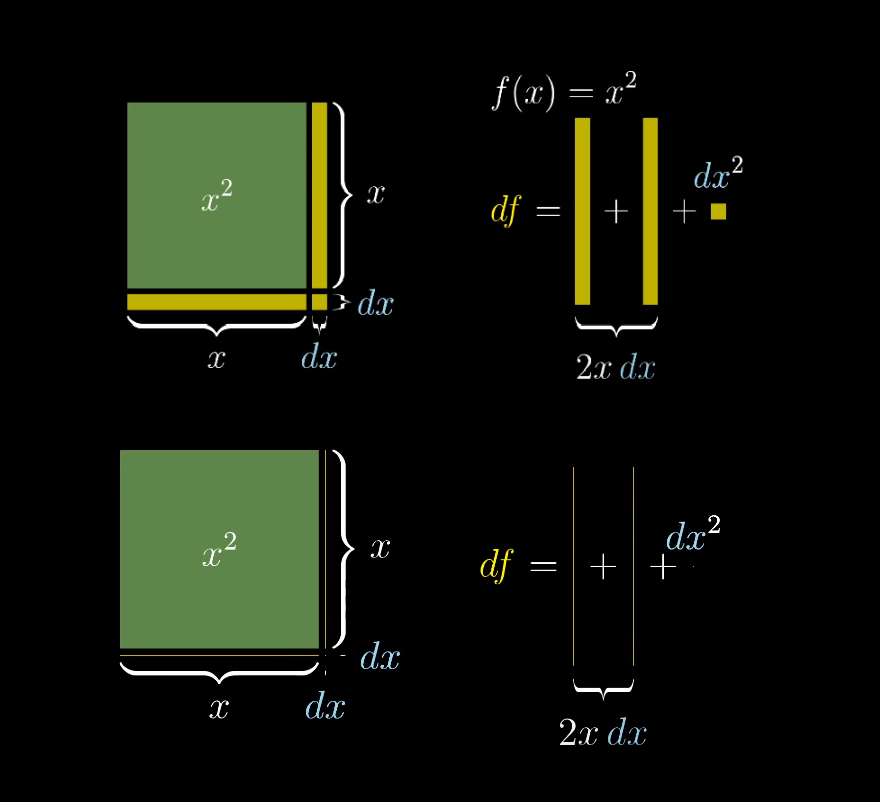[그림] $x^2$을 기하학적으로 미분해보자.
- $x^2$을 정사각형으로 그리면 위와 같다. 변의 길이($x$)가 변하면, 사각형의 넓이는 $x$의 제곱꼴로 변한다
- 이 때, 독립변수 $x$는 정사각형의 한 변이 되고, 종속변수 $y(x^2)$는 정사각형의 넓이가 된다.
- 이 때 독립변수 $x$를 $x + dx$꼴로 키우게 되면, 위와 같은 일이 벌어지는데, 우리가 생각했던 $df$는
- 원래 $x$를 조금 변화시킬 때, $x^2$이 변하는 양이기 때문에, 위 그림에서 보면 노란색 길다란 막대기 2개와
- 매우작은 점과같은 사각형 하나를 포함하게 된다. 그런데 이 길다란 막대기는 $x \times dx$의 넓이를 가지고,
- 2개이므로 곱하면 $2xdx$, 작은 사각형은 $dx^2$이 되고 이 모든 것을 합친게 $df$(늘어난 넓이)가 된다.
- 도함수는 $\lim_{h \to 0}\frac{df}{dx}$이기 때문에, $df = 2xdx + dx^2$을 $dx$로 나누면 결과는 아래와 같다.
- $\frac{df}{dx} = 2x + dx$이다. 그러나 $lim_{dx\to0}$이기 때문에, $dx$는 거의 사라지고 정답은 $2x$가 된다.
- 실제로 저 노란색 부분에서 $dx$의 크기를 거의 0과 같이 줄이면 길이가 x인 가느다란 2개의 실을 사각형에
- 붙인 꼴을 상상할 수 있다. (그림의 아랫부분에서 점은 거의 사라지고 가느다란 실 2개가 남는 것을 볼 수 있다)
3. 한발 더 나아가서 ($x^3$)
[그림] $x^3$을 기하학적으로 미분해보자.
- 위와 같은 방법으로 똑같이 $x^3$도 미분할 수 있다. 기존 부피에 추가되는 부피를 계산해보자.
- 저 노란색 얇은 직육면체는 가로(x), 세로(x), 높이(dx)를 곱해서 $x^2dx$가 되는데 세개의 면에서 생기므로
- 그 부피를 모두 합치면 $3x^2dx$이다. 또한 가로(x), 세로(dx), 높이(dx)를 곱한 막대도 3개가 생기고,
- 최종적으로 가로(dx), 세로(dx), 높이(dx)인 아주 작은 정육면체까지 생겨서 이들의 합이 $df$가 된다.
- 우리가 원하는 것은 $\frac{df}{dx}$이기 때문에 $df = 3x^2dx + 3xdx^2 + dx^3$을 $dx$로 나눠주게 되면,
- $\frac{df}{dx} = 3x^2 + 3xdx + dx^2$이 되고, $lim_{dx\to0}$으로 보낼 것이기 때문에 결과는 $3x^2$이 된다.
- 실제로 저기에서 마찬가지로 $dx$를 거의 0에 가깝게 줄이면 정육면체의 3개 표면에 종이같이 얆은 면 3장을
- 덧댄것과 크기가 같아지고 그 것은 $x^2$을 3장 덧댄것으로 $3x^2$이라고 할 수 있다.
4. 일반화 ($x^n$)
- 이제 우리는 다항함수에서 미분이 $x$를 $x + dx$로 키웠을 때, $\frac{df}{dx}$를 계산하는 것이라고 잘 알고 있다.
- 만약 3차원 이상의 $x^n$을 미분한다면 더 이상 시각적으로 볼 수 없다. 때문에 여기선 수식을 이용한다.
- $x^n$에서 $x$를 $x + dx$처럼 키우면, $(x + dx)^n$이 되고 $(x+dx)(x+dx)(x+dx) ... (x+dx)$가 된다.
- 이 문제는 이항정리로 풀어낼 수 있는데, 가장 큰 $x^n$은 모든 $(x+dx)$에서 $x$만 선택한 것이기 때문에,
- $nC0$이 되어 계수가 1이 되고, 두번 째 항에서는 n개의 $(x+dx)$에서 $dx$를 하나만 선택하는 것이기 때문에
- $nC1$이 되어 계수는 n이 된다. 그러나 그 뒤부터는 $dx$를 두개 이상 선택하게 되고, 나중에 $dx$로 나누면
- 전부 0과 같이 작아질 것을 알기 때문에 더 이상 계산하지 않는다. 결론적으로 $df$는 새로 넓어진 영역이고
- 이는 x로 만든 기존 넓이$(x^2)$와 x를 (x+dx)놓고 만든 넓이$(x^2 + nx^{n-1}dx + dx^2(...))$의 차이이기 때문에
- $nx^{n-1}dx + dx^2(...)$이 되고, 이를 $dx$로 나누면 $nx^{n-1}$이 됨을 알 수 있다.
5. Reference