1. 순간의 변화량??
- 우리는 일반적으로 "미분함수" 혹은 "도함수"는 "순간의 변화량"이라고 학교에서 배웠다.
- 그런데, "변화"라는 것은 시간이 흐를러서 무언가가 변하는 것이다.
- 그런데 "순간"이라는 것은 시간이 흐르지 않는 순간 그 자체이므로 변화할 시간이 없어진다.
- 그런데도 "순간의 변화량"이라니, 이게 도대체 무슨말일까...?
2. 움직이는 자동차를 생각해보자.
[그림] 자동차의 움직임
- 자동차가 위와 같이 움직인다고 생각해보자. 처음 출발할 때는 가속하느라 속도가 점점 빨라지고,
- 중앙 지점을 넘어서면 멈추기 위해 속도가 점점 느려진다.
[그림] 시간에 따른 총 이동량 그래프
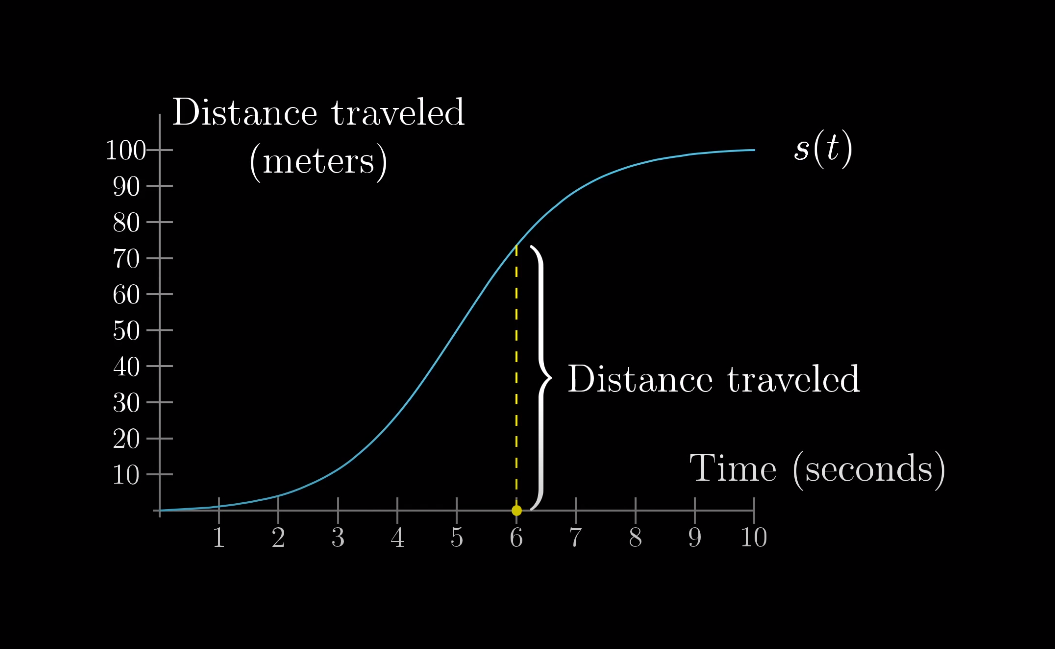
- 그러면 우리는 자동차가 움직인 시간과 거리의 그래프를 생각할 수 있다.
- x축 = t는 Time은 시간이고, y축 = s는 시간에 따른 총 이동량이라고 생각해보자.
- 만약 t = 6이라면, s는 6초까지 총 이동한 거리가 되는 그런 그래프이다.
- 이 곡선은 처음에는 완만하다. 자동차가 처음에는 가속하느라 느리기 때문이다.
- 그리고 중간지점에는 최고 속력에 도달했다가, 다시 정지하기 위해 점점 느려진다.
3. 속력(Velocity)를 고려해보자.
[그림] 속력의 그래프로 표현하면?
- 우리가 이 자동차의 속력의 그래프를 표현하면 위 처럼 녹색 그래프로 표현 할 수 있다.
- t = 0일 때 속력은 0이다. 운동을 진행하면서 자동차는 최대속력을 향해서 달려가고,
- 그러면서 초당 움직인 거리(속력)은 커져가고, 그러다가 다시 0m/s까지 감소한다.
- 우리는 파란색 그래프와 녹색 그래프 사이의 관계가 궁금한 것이다. 그러나 그전에 "속력"은 뭘까?
4. 순간 시점의 속력? (실제론 불가함)
[그림] 이 사진속 자동차의 속력은?
- 순간 시점, 즉 이 사진 속처럼 변화가 없는 이 자동차의 속력을 생각할 수 있을까? (대답은 NO)
- 속력을 측정하기 위해 필요한 것은 "두 특정 시점"이다. 두 시점 사이에 움직인 거리를 측정해야한다
[그림] 특정 시점 사이의 속력
- 이렇게 속력을 계산하려면 특정 시점(4초 to 5초) 사이에 흐른 시간(1초)동안에 움직인 거리를 계산하면
- 이 것이 바로 우리가 알고 있는 "속력"의 개념이다. 바로 주어진 시간동안에 움직인 거리를 의미한다.
- 그러면 단일 시간 t에서의 속력은 무엇일까? (이상하지 않은가? 0초동안 이동한 거리는 당연히 0이다...)
- 우리는 단일 시간 t에서 속력을 계산하고싶은데, 실제로 속력을 계산하려면 두 시점이 필요하다.
- 이상한 느낌이 드는게 당연하다. 이 것은 미적분을 발견하고 정리한 수학자들도 동일하게 했던 고민이다.
[그림]
- 우리가 실제로 속력계를 만든다고 가정하면, 매우 짧은 시간(0.1초)동안의 움직인 거리를 측정하여
- 속력계를 만들 수 있다. 이렇게 하면 우리가 지금 말하고 있는 "도함수"의 역설을 해결할 수 있다.
- 매우 짧은 시간 0.1초를 $dt$로, 그간에 움직인 거리를 $ds$로 놓고 계산하면, 그게 바로 속력이다
5. 속력은 사실 거리의 기울기이다. (same with 도함수는 함수의 기울기이다)
[그림] 속력은 사실 거리의 기울기이다.
- 이 작은 $dt$와 그에 따라 움직인 거리인 $ds$를 확대해보면 위와 같다.
- 그리고 속력의 "정의"인 $\frac{ds}{dt}$는 이 함수의 기울기가 된다. (직관적으로 이해가 안간다)
- 생각해보자. 우리가 매일 이야기하는 $y = 2x$꼴의 그래프를 생각해보자.
- x에 1을 넣으면 y=2가나오고, x에 5를 넣으면 y=10이 나온다. 즉, 이 함수는 "2"만큼 기울어져있다.
- $y = 2x$에서 우항을 x로 나눠주면 $\frac{y}{x} = 2$가 되고, 기울기는 $\frac{y}{x}$가 된다.
- 그런데 위 사진의 그래프에서는 y=s(거리)이고 x=t(시간)이기 때문에 $\frac{ds}{dt}$는 기울기가 된다.
[그림] 속력은 사실 거리의 도함수이다.
- 다시 위를 봤을 때, 거리함수 $s(t)$가 있을 때, $dt = 0.1$에 대하여 속력 $v$ = $s(3) - s(3.1) / 0.1$이고,
- 이 것은 우리가 이전 글에서 봤던 도함수의 나이브한 정의 $\frac{f(x+h) - f(x)}{h}$와 정확히 일치한다
- 실제 도함수의 정의는 사실 $\lim_{h\to0}$이 추가되어야 하기 때문에 나이브한 정의라고 한 것이다.
6. $dt \to 0$으로 보내면 어떤일이 벌어질까?
[그림] $dt \to 0$으로 갈때,
- $dt$가 만약 0은 아니지만 0에 매우매우매우 근접한 어떤 상수가 된다면 (ex. 0.0000000 ... 0001)
- 그러면 $\frac{s(t + dt) - s(t)}{dt}$는 마치 접선의 기울기 처럼 보이게 될 것이다.
- 실제 도함수의 정의인 $\lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$는 두 점사이 기울기가 아니라
- 사실상 접선의 기울기가 된다. 이 때 $dt$는 0도 아니며 무한히 작은 어떤 값도 아니다.
- 충분히 유한하게 작지만 거의 0에 근접한 그런 수라고 생각해야한다. (0이면 존재 불가능)
- 실제로 수학에서는 $d$를 그렇게 써왔다. d는 0은 아니고, 무한히 작지도 않지만, 유한하게 작으며
- 0에 계속하여 근접하고, 사실상 0과 같은 그런 엄청나게 작은 수 (이를 극한이라고 하는데 다음에 알아보자)
- $dt$는 0은 아니지만 사실상 0과 같은 그런 수라고 생각하고 계산하면 수식도 엄청나게 깔끔하고 편해진다.
7. 도함수의 계산
[그림] 도함수 계산
- 위를 보면 왜 $dt$가 0은 아니지만 0처럼 생각하면 편하다고 하는지 말해준다.
- 위에서 $s(t) = t^3$이라는 함수가 있을 때 t=2지점에서 도함수를 구하면
- $\frac{s(t + dt) - s(t)}{dt}$는 위와 같이 계산된다. 최종적으로 $3(2)^2 + 3(2)(dt) + (dt)^2$이 남는데,
- 여기에 $dt=0$이라고 생각하면 뒷부분이 다 날아가서 굉장히 깔끔한 $3(2)^2$만 남게 된다.
8. 결론 : 도함수의 역설
- 도함수의 역설은 사실이다. 도함수의 개념 자체에 모순이 존재하는 것이 맞다.
- "순간 변화량"에서 "변화"는 시간에 따라 변함을 의미하고 "순간"은 시간의 흐름이 없음을 의미한다.
- 우리가 위에서 쭉 알아본 바로는 사실은 이 변화율은 완벽한 "순간" 혹은 "찰나"라고 말하긴 어렵지만,
- "순간"에 거의 도달할 정도로 근접하여 거의 순간과 비슷하다고 할 수 있는 근사치는 된다라는 것이다.
- 그런데 이 근사치가 진짜 엄청나게 작으니 계산하거나 그럴 땐 그냥 0으로 퉁치면 편하다라는 것도 알았다.
- 그러나 절대로 이 것이 0은 아니다. 절대 0은 아닌데 진짜 거의 0과 비슷하게 근사한 값이라는 것이다.
(사실 측정가능한 0이라는 시간은 애초에 있을 수 없다. 그걸 플랑크시간이라고 하는데 그게 뭐냐면 ..)
9. Reference