1. 2레벨 구현
- 우리가 어떤 SOm함수나 POM함수를 회로로 구현할 때 2레벨로 구현할 수 있다
- f(a, b, c) = SOm(2, 3, 5, 7)이라는 함수가 있을 때, 카르노맵을 활용해 2레벨로 구현보면,
- 아래와 같이 구현할 수 있다. SOm이기 때문에 AND - OR로 구현된다.

2. NAND to ALL
- 어떤 함수를 구현함에 있어서 곱은 AND로 합은 OR로 리터럴은 NOT으로 표현가능하다.
- 이 말은 즉, AND, OR, NOT만 있으면 이 세상에 있는 모든 불리안 함수를 구현 가능하다.
- 그런데 우리가 이전 글에서 알아본 NAND게이트나 NOR게이트는 AND, OR, NOT으로 변환 가능하다
- 결론적으로 NAND게이트만으로 혹은 NOR게이트만으로 모든 함수의 구현이 가능하다.
1) NAND to NOT (1)

- 두 신호를 동일하게 NAND게이트에 입력하면 NOT과 동일한 효과를 볼수 있다
- 이를 통해 회로를 위처럼 연결해서 NOT게이트를 만들 수 있다.
2) NAND to NOT (2)

- 마찬가지로 한쪽 신호를 1로 고정했을 때, 어떤 값이 들어오면 NOT과 동일한 효과를 볼 수 있다
- 이렇게 NOT회로를 구현할 수 도 있다.
3) NAND to OR

- 위와 같이 NAND의 두 입력에 인버터를 붙이면 OR게이트가 된다.
- 이는 드모르간 법칙에서 기인한 것인데 NOT (AB) = NOT A + NOT B와 동일하기 때문이다
- 이 때 다시 NOT A와 NOT B에 NOT을 취해주면 A + B로 OR게이트가 된다.
4) OR to NAND

- 마찬가지로 OR 게이트를 NAND게이트로 변환할 수 도 있다
- 같은 방식으로 입력에 인버터를 붙이면 OR게이트는 NAND게이트가 된다.
5) NAND to AND

- NAND게이트의 출력에 다시 한번 인버터를 붙여주면 AND 게이트가된다.
- 이렇게 NAND게이트 하나로 AND, OR, NOT게이트가 모두 구현 가능하다
6) Only NAND

- 이러한 성질을 이용해서 위 SOm 2레벨 함수를 NAND게이트만 써서 구현할 수 있다.
- 어떤 선로에 인버터를 두번 태우면 원래값과 완전히 같기때문에
- 위쪽 AND에서 OR로 가는 선로에 인버터 두번 그리고 아래쪽 AND에서 OR로 가는 선로에
- 인버터를 두번 붙여주면 결과는 같지만, 게이트는 모두 NAND게이트로서 해석될 수 있다.
2. NOR to ALL
- 마찬가지로 NOR 게이트로도 AND, OR, NOT을 모두 구현할 수 있다.
1) NOR to NOT (1)

- NAND게이트와 마찬가지로 NOR게이트도 같은 입력 두개를 넣으면 NOT게이트가 된다.
2) NOR to NOT (2)

- 하나의 입력을 0으로 고정하면 NOR게이트는 NOT게이트로 사용할 수 있다.
3) NOR to AND

- 마찬가지로 NOR게이트의 두 입력에 모두 인버터를 붙이면 AND게이트가 된다.
4) AND to NOR

- 그 반대도 역시 성립한다.
5) NOR to OR

- NOR의 출력에 인버터를 붙이면 당연히 OR게이트가 된다.
6) With NOR / NAND
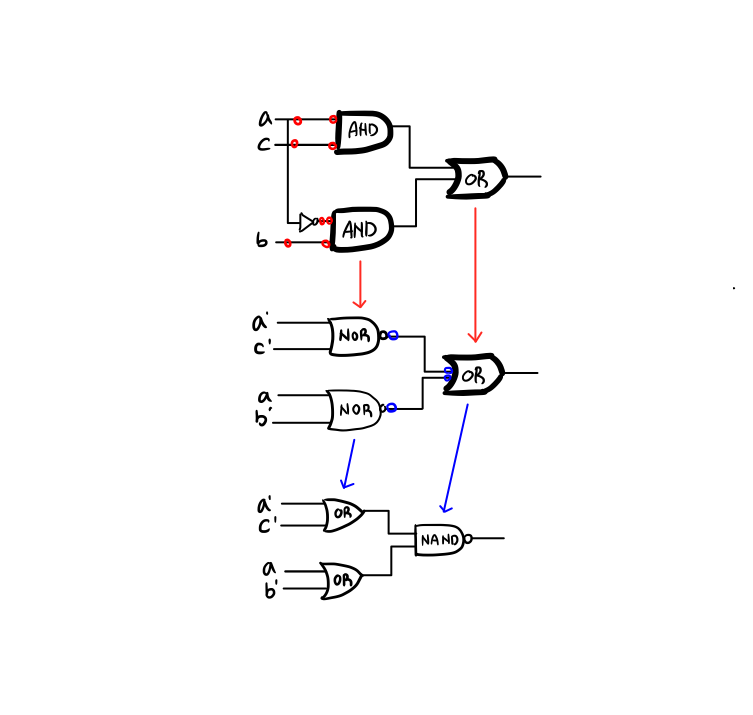
- 이런 성질들을 이용하면 같은 함수를 매우 다양한 게이트로 구현할 수 있다.
3. Minterm to Maxterm
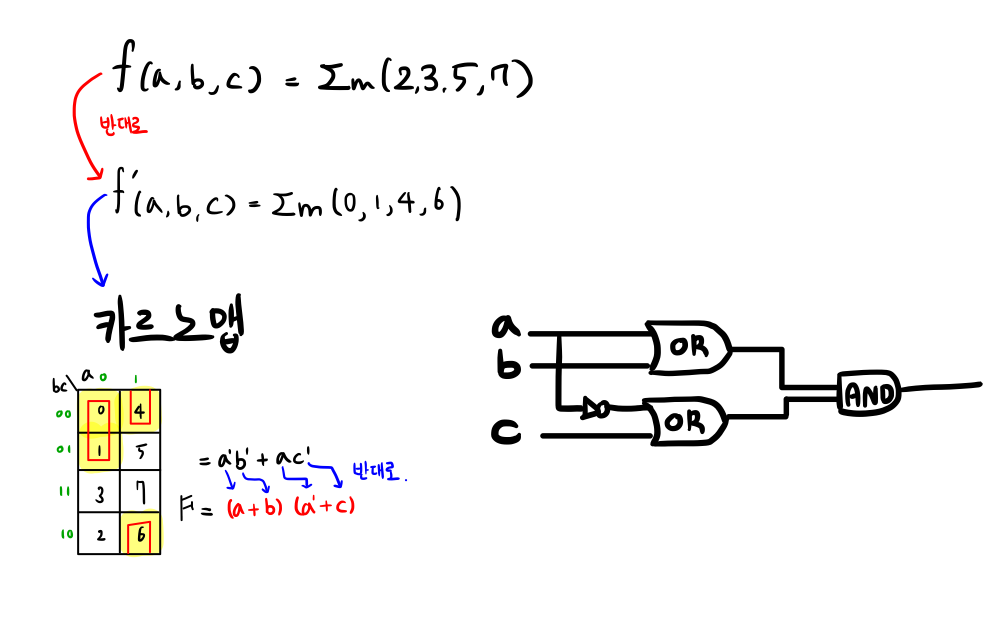
- 위와 같이 minterm을 maxterm으로도 바꿔서 구현 할 수 있다.
- som(2, 3, 5, 7)의 반대인 som(0, 1, 4, 6)을 카르노맵으로 구현한 뒤에,
- som의 각 minterm들의 부호를 전부 바꾸고 OR을 AND로 바꿔주면 Maxterm이된다.
- 이렇게 하면 오른쪽과 같이 다시 2레벨로 Maxterm을 구현하는게 가능해진다.
- 기존 som(2, 3, 5, 7)과 결과로 만들어진 POM함수는 동일한 함수이다 (벤다이어그램 그려보기)

2) Maxterm with NAND / NOR

- 위에서 이용한 NAND, NOR들의 특성을 이용해 회로를 매우 다양하게 구현할 수 있다.
4. Reference
'논리회로' 카테고리의 다른 글
| 해저드(Hazard) 와 해저드 프리(Hazard-Free) 함수 (0) | 2020.05.22 |
|---|---|
| XOR게이트, XNOR게이트, NOT게이트 만들기 (0) | 2020.05.19 |
| Quine - McClusky 방법 (2) - 예시 (0) | 2020.04.21 |
| Quine - McClusky 방법 (1) (1) | 2020.04.21 |
| 카르노 맵 (6) - Don't Care (무관항), 그레이 코드 쓰는 이유 (0) | 2020.04.20 |
| 카르노 맵 (5) - 4 변수 (0) | 2020.04.20 |
| 카르노 맵 (4) - Implicant 방식 예제 (0) | 2020.04.20 |