1. Combination의 정의
1) 조합의 정의
- 조합이란 주어진 원소를 이용해 만들 수 있는 "집합"의 수 (순서가 없는건 집합의 정의!)
- 공식보지 말고 원리로 이해해보자! 5명 중에서 3명을 뽑는 조합의 수를 구해보자.
- 처음에 만약 순서 있게 뽑으면 5 x 4 x 3이 된다 (순열) 이 때 중복되는 집합의 수로 나눠주면 된다
- (이전 글에서 공부했던 "반복이 있는 순열"과 비슷한 원리로 한번 접근해보자는 것이다)
- 중복되는 집합의 수는 3개의 원소로 만들수 있는 모든 집합이다 = 3 x 2 x 1 = 3!
2) 이게 뭔 X소리야?

- 무슨말이냐면, (a, b, c, d, e)중에서 최종적으로 a, b, d를 뽑았는데, a, b, d로 만들 수 있는
- 모든 경우의 수 (a, b, d), (a, d, b) , ... (d, b, a)를 전부 세서 나누면 중복된 경우를 모두 뺄 수 있다는 것.
- 3개의 원소로 구할 수 있는 모든 경우의 수는 3!이기 때문에 (3개중 3개 뽑기 : 순열)
- 최종적으로 5 x 4 x 3 / 3!으로 나눈다. 이 것을 다시 쓰면 5! / 2! * 3!과 같다.
3) 표기법, 읽는법, 기타
- 그리고 확률론에서는 이것을 5C3 혹은 컬럼벡터처럼 (5, 3)으로 표기한다. (세로로 써야한다)
- 또, 이 것을 읽을때는 nCr이라고 읽지 않고 n Choose r이라고 읽는다 (교수님이 그렇게 읽는다)
- 참고로 5C5나, 5C0은 1이다. (5개의 원소가 있을 때 5개/0개를 뽑아서 만들어지는 집합은 1개)
- 또한 nCr과 nC(n-r)은 동일하다, 음.. 5명중 1명 당첨과 5명중 4명 비당첨이 같은 이치이다.
2. Permutation vs Combination
- Permutation : 순서가 있다 (주어진 원소로 만들어지는 배열의 개수)
- Combination : 순서가 없다 (주어진 원소로 만들어지는 집합의 개수)
- 자료구조에서 Set과 Array의 차이라고 보면 된다. (Set은 중복허용X, 순서가 없다)
- 문제를 봤을 때, 그게 순열이나 조합이라고 안써져있다. 우리가 문제 보고 생각해야한다.
- e.g. 대의원2명 vs 반장,부반장 => 대의원(순서없음) = 조합 / 반장부반장(순서있음) => 순열
3. 문제 풀이
1) 20명중 대의원 4명 뽑기 => 20! / 4! * 16!
2) 남자7명중 3명 , 여자 5명중 2명 뽑기 => 7C3 * 5C2
이 때, 남자 둘이 싸워서 같이 뽑히고 싶지 않다고 한다면? => (7C3 - 5C1) * 5C2
왜? : A,B가 싸웠다면 [A, B, _]처럼 A, B를 픽스해놓고,
ㅁ나머지 _ 자리에 올 수 있는모든 경우를 빼주면 된다.
7명중 5명이 남았기 때문에 5C1이 되고 7C3에서 빼주면 된다.
3) 안테나문제 해답 :
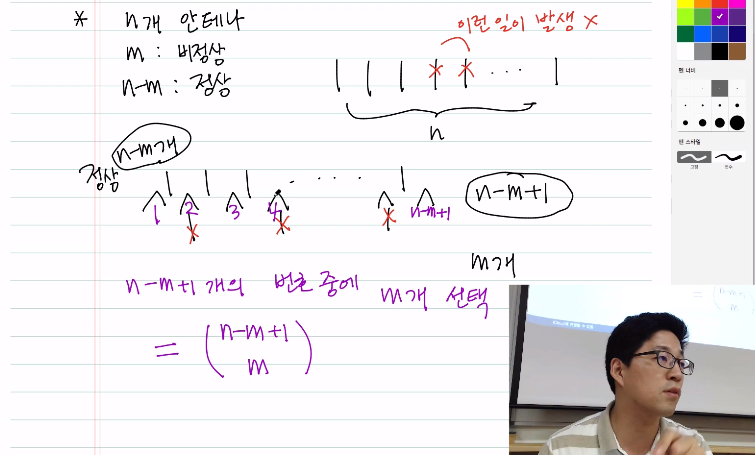
4. Reference
'확률론' 카테고리의 다른 글
| 경우의 수 (5) - 다양한 테크닉 (1) | 2020.05.25 |
|---|---|
| 경우의 수 (4) - 이항정리 (0) | 2020.05.12 |
| 경우의 수 (2) - 순열 (0) | 2020.05.06 |
| 경우의 수 (1) - 경우의 수를 세는 기본 법칙 (0) | 2020.05.06 |