1. 알고리즘 개요
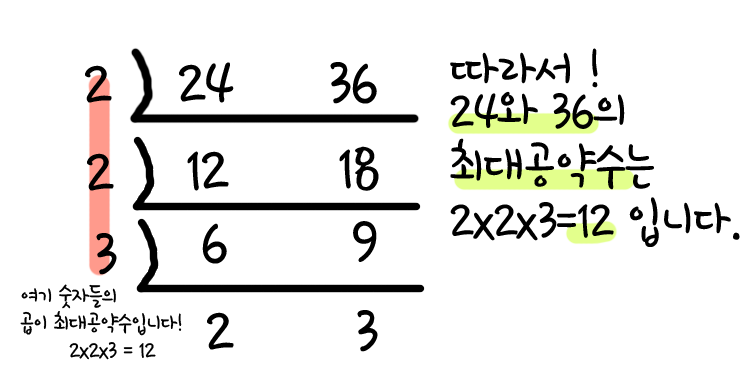
"유클리드 알고리즘"이라고 해서 말이 어려워 보이는데, 사실 두 수의 최대공약수를 구해내는 알고리즘이다. 우리가 손으로 최대공약수를 구할 때는 위의 [그림]과 같이 소인수분해(두 수를 쓰고 두 수의 공약수 중에서 서로소인 수를 계속해서 써내려가는 것)를 통해 계산한다. 그러나 이러한 방법은 인간의 직관에 의한 것으로 기계적으로 설계하기에 적합하지 않다. 때문에 우리는 유클리드 호제법을 이용하여 최대공약수를 구하는 알고리즘을 설계한다.
u>v인 두 정수 u, v의 최대공약수를
구하는 함수를 gcd(u, v)라고 할 때,
1. gcd(u, v) = gcd(u-v, v)
2. gcd(u, v) = gcd(v, u)
3. gcd(u, 0) = u
유클리드 알고리즘의 기본 가정은 위와 같다. u > v인 두 정수 u와 v의 최대공약수를 구할 때, u와 v의 최대공약수는 u - v와 v의 최대공약수와 동일하며, 어떤 수 u와 0 사이의 최대공약수는 u가 된다. 이를 정리하면 아래와 같다. 이 가정을 이용하여 유클리드 알고리즘을 설계한다.
Euclidian Algorithm
(1) 만약 v가 u보다 커지면
v와 u를 바꾼다.
(2) u = u - v로 대체한다.
(3) 만약 v가 0이면 u를 리턴하고,
아니라면 (1)로 돌아간다.
gcd(u, v) = gcd(u - v, v)이기 때문에, u = u - v로 대체해준다. 이렇게 하게 되면 u가 계속해서 v만큼 감소하게 되고, u가 v보다 작아질 때, 둘을 교체해서 다시 u가 v보다 커지게끔 해준다. 이러한 방식으로 계속해서 u를 작아지게 해주면, gcd(20, 10) = gcd(10, 10) = gcd(0, 10) = gcd(10, 0)(u와 v스왑) 과 같이 나중에 v가 0이 되게 된다.이런 경우, u와 0과의 최대공약수는 u이기 때문에, u를 리턴하고 알고리즘을 종료한다.

그런데 다시 생각해보면, u - v 를 계속해서 진행하여 나온 결과는 사실 u에서 v에게 나머지 연산(mod)을 한 것과 동일하다. 만약 u가 매우 크고, v가 매우 작다면, (e.g. u = 100000, v = 30) u에서 v를 계속해서 빼야하고 너무 많은 반복을 수행해야한다. 때문에, 이런 경우에는 u에서 v를 나머지 연산하여 한번에 결과를 계산하는 것이 더욱 효율적이다. 이렇게 나머지 연산을 사용하여 수정된 알고리즘은 다음과 같다.
Euclidian Algorithm (MOD)
(1) 만약 v가 u보다 커지면
v와 u를 바꾼다.
(2) u = u % v로 대체한다.
(3) 만약 v가 0이면 u를 리턴하고,
아니라면 (1)로 돌아간다.
이렇게 나머지 연산자를 사용하여 처음부터 나머지 값을 구해서 연산을 수행하면 보다 적은 반복으로 유클리드 알고리즘을 구현할 수 있다. (수학쪽에서 유클리드 알고리즘을 부를 때는 이 나머지 연산을 베이스로 한 방식으로 기본으로 한다.)

2. 소스코드
#include <cstdio>
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
/**
* 최대 공약수 (Greatest Common Divider) 알고리즘
* 1. GCD(u, v) = GCD(v, u) : 교환법칙 성립
* 2. GCD(u, v) = GCD(u-v, v) (단, u > v)
* 3. GCD(u, 0) = u : GCD의 항등원은 0
* */
int gcd(int u, int v) {
if (v > u) swap(&u, &v);
if (v == 0) return u;
else return gcd(u - v, v);
}
/**
* 위 gcd 알고리즘을 보면, swap이 일어나기 전까지
* u에서 v를 지속적으로 빼는데, 이는 곧 u % v 와 같음
*
* 1. original gcd ex) 100, 30
* 100 - 30 = 70
* 70 - 30 = 40
* 40 - 30 = 10
* 10 < 30 => swap
* 30 - 10 = 20
* 20 - 10 = 10
* 10 - 10 = 0
* return 10;
*
* 2. improved gcd ex) 100, 30
* 100 % 30 = 10
* 10 % 30 = 10
* 10 % 10 = 0
* return 10;
* */
int improved_gcd(int u, int v) {
if (v > u) swap(&u, &v);
if (v == 0) return u;
else return gcd(u % v, v);
}
int main() {
printf("%d\n", gcd(10, 30)); // 출력 : 10
printf("%d\n", improved_gcd(10, 30)); // 출력 : 10
return 0;
}
github.com
전체 소스코드는 Github에서 확인하실 수 있습니다.
3. 증명
1) 어떤 수 $A \geq B$인 $A$와 $B$가 있을 때, $A = qB + r$ 과 같이 나타낼 수 있다.
($q$는 몫, $r$은 나머지)
2) $gcd(A, B) = d$ 라고 하면, $A = ad, B = bd$이다. (이 때, $a$ 와 $b$는 서로소이다.)
3) 이때, $A = qB + r$이므로, $r = A - qB = ad - bdq = (a - bq)d$ 이다.
4) 여기서 $B = bd$이고, $r = (a-bq)d$ 이므로, $d$는 $B$와 $r$의 공약수 중 하나이다
5) 이 때, $B$와 $r$의 최대공약수를 $c$ 라고 한다면, $d$는 공약수이기 때문에, $c \geq d$이다.
6) 또 다른 서로소 $s$와 $t$를 도입하여, $B = cs, r = ct$라고 하면, $A = qB + r = scq + ct = (sq+t)c$이다. 이 때, $c$는 $B = cs$ 와 $A=(sq+t)c$ 이기 때문에, $A$와 $B$의 공약수인 것을 알 수 있다.
7) 따라서 $c$는 $A$와 $B$의 최대공약수인 $d$의 약수이고, $d \geq c$임을 알 수 있다.
8) 결론적으로, $c \geq d$이고, $d \geq c$이기 때문에, $d = c$이고 즉, $gcd(A, B) = gcd(B, r)$이다.
4. Reference
유클리드 호제법 정리 / 증명
알고있던 유클리드의 호제법이 생각이 나지 않아서 다시 한번 정리 해둔다.(열강 도전 프로그래밍 ONE을 보다가) 유클리드 호제법이란. A >= B인 어떤 두 정수 A와 B가 있을 때(A = Bq + r로 나타낼 수 있다.) A와..
nukeguys.tistory.com
'알고리즘' 카테고리의 다른 글
| 재귀 (3) - 하노이 탑 (Tower of Hanoi) (0) | 2020.02.04 |
|---|---|
| 재귀 (2) - 피보나치 수열 (Fibonacci Series) (0) | 2020.02.04 |
| 재귀 (1) - 개요 (0) | 2020.02.04 |
| 미로 알고리즘 - 우선법 (Right Hand on Wall) (0) | 2020.01.21 |
| 소수 (2) - 에라토스테네스의 체 (Sieve of Eratosthenes) (0) | 2020.01.10 |
| 소수 (1) - 소수 판별하기 (0) | 2020.01.08 |
| 어 라 루스 (A La Russe) (0) | 2020.01.03 |