1. 알고리즘 개요
하노이의 탑은 3개의 기둥과 크기가 각각 다른 N개의 원판이 주어졌을 때 1번 기둥의 모든 원판을 3번 기둥으로 옮기는 일종의 퍼즐게임이다. 원판을 옮기기 위해 2번 기둥을 사용할 수 있고, 작은 원판 위에는 큰 원판이 올라올 수 없다는 제약조건이 있다. 아래의 영상을 보면 하노이의 탑에 대해 쉽게 이해할 수 있을 것이다.
2. 하노이의 탑 문제의 최소 움직임 수
이론적으로 하노이의 탑 문제는 N개의 원판이 주어졌을 때, $2^N - 1$번의 움직임만에 해결할 수 있다. (이보다 적은 횟수의 움직임으로는 해결할 수 없다) 실제로 퍼즐을 풀어보며 이 것이 맞는지 확인해보자.
N = 1
(1번)
1 → 3
N = 2
(3번)
1 → 2
1 → 3
2 → 3
N = 3
(7번)
1 → 3 , 1 → 2 , 3 → 2
1 → 3
2 → 1 , 2 → 3 , 1 → 3
위의 움직임들은 각각 N이 1, 2, 3일 때의 최단 경로 해법이다. 실제로 N개의 원판이 주어졌을 때, $2^N - 1$번이 소요되는 것을 확인할 수 있다.
3. 하노이의 탑 해법
하노이의 탑 문제의 최소 움직임 해법을 찾는 방법은 생각보다 간단한다. 가장 큰 원판을 1번 기둥에 놓고 나머지 모든 원판을 2번 기둥으로 움직이다. 그리고 가장 큰 원판을 3번으로 움직이고, 나머지 원판들도 3번으로 움직인다. 아래의 그림을 보면 더 쉽게 이해할 수 있을 것이다.
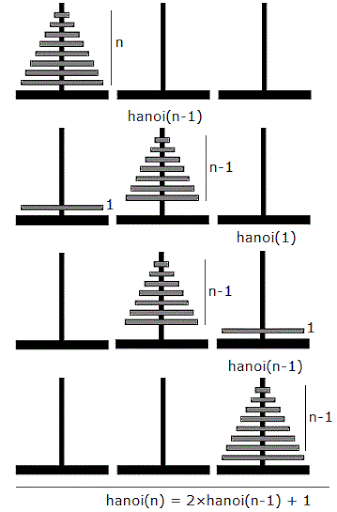
이제 왜 최소 움직임 수가 $2^N - 1$인지 알 수 있다. 4개의 원판이 주어졌을 때, hanoi(3)를 2번 기둥으로 옮기고, 가장 큰원판을 3번 기둥으로 옮기고 2번 기둥에 있던 hanoi(3)을 다시 3번 기둥으로 옮긴다. 즉, hanoi(3)을 두번 옮기고 큰 원판을 1번 옮기는 것과 같다. 실제로 hanoi(4) = 15이고 hanoi(3) = 7이다. 때문에 7 + 1 + 7 = 15가 된다. 이 관계를 단계별로 나타내면 다음과 같다.
1 = 1
1 + 1 + 1 = 3
3 + 1 + 3 = 7
7 + 1 + 7 = 15
15 + 1 + 15 = 31
31 + 1 + 31 = 63
...
이를 일반화 시키면 최소 움직임의 횟수가 $2^N - 1$가 됨을 알 수 있다.
4. 소스코드
#include <stdio.h>
void move(int from, int to){
printf("%d => %d\n", from, to);
}
void hanoi(int n, int from, int by, int to){
if(n == 1){
move(from, to);
}else{
hanoi(n-1, from, to, by);
move(from, to);
hanoi(n-1, by, from, to);
}
}
int main() {
hanoi(3, 1, 2, 3);
return 0;
}
재귀함수를 이용하면 위 처럼 매우 직관적이고 쉽게 하노이의 탑 알고리즘을 구현할 수 있다.
모든 소스코드는 Github에서 확인할 수 있습니다.
gusdnd852/TIL
Source code collections of my blog 📝. Contribute to gusdnd852/TIL development by creating an account on GitHub.
github.com
5. Reference
'알고리즘' 카테고리의 다른 글
| 재귀 (6) - 파일 탐색 (File Finding) (0) | 2020.02.04 |
|---|---|
| 재귀 (5) - 프랙탈 트리 (Fractal Tree) (0) | 2020.02.04 |
| 재귀 (4) - 플러드 필 (Flood Fill) (0) | 2020.02.04 |
| 재귀 (2) - 피보나치 수열 (Fibonacci Series) (0) | 2020.02.04 |
| 재귀 (1) - 개요 (0) | 2020.02.04 |
| 미로 알고리즘 - 우선법 (Right Hand on Wall) (0) | 2020.01.21 |
| 소수 (2) - 에라토스테네스의 체 (Sieve of Eratosthenes) (0) | 2020.01.10 |