1. Circular Queue (원형 큐)
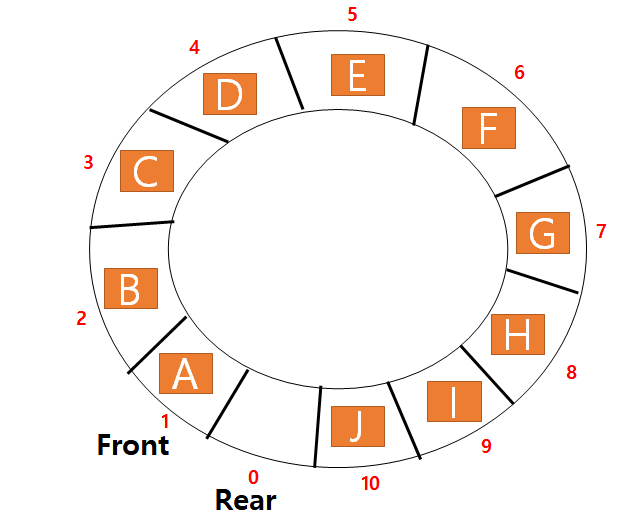
- 원형큐는 배열의 맨 앞과 맨 뒤를 이어붙인 큐 구조라고 생각하면 좋다.
- 그래서 위와같이 10번 인덱스까지 모두 채웠을 때,
- 그 뒤에 비어있는 0번 인덱스에 값을 채울 수 있게 설계하였다.
- 배열의 Front와 Rear를 회전시킨다는 Novel한 아이디를 사용하여 선형 큐의 문제를 해결한 것이다.
2. Modular(%) for Rotating
Front와 Rear를 회전시키기 위해서 모듈러연산(%)을 사용한다.
아래 설명한 예시를 보면서 왜 이렇게 해야하는지 이해해보자.
enqueue: rear = (rear + 1) % capacity;
dequeue: front = (front + 1) % capacity;
- 위 그림처럼 capacity=11인 배열의 예시를 생각해보자.
- 만약 10번째 인덱스까지 모두 채웠으면 다음 Rear는 11이 아니라 0이 되어야한다.
- 원래대로면 rear(10) + 1 = 11이기 때문에 index 오류지만. % 11을 해주면 0으로 돌아온다
- 마찬가지로 12 % 11 = 1이고, 13 % 11 = 2이며, 14 % 11 = 3이다.
- 이런식으로 0 ~ 10까지 돌고나서, 11을 넘어가면 % 11로 0부터 다시 시작하게 만들어준다.
- dequeue도 마찬가지 이다. 10번째 인덱스에 있는 원소를 dequeue하면 front가 1증가해서,
- 원래는 11이 되어야하지만 % 11을 해줘서 다음 지울 위치가 0번 인덱스라는 것을 알 수 있다.
3. 그렇다면 Size와 Full, Empty는?
1) Size = (capacity + rear - front) % capacity
- 기존에는 Size를 Rear - Front로 계산했다. 그러나 이제는 Rear가 Front보다 작아질 수 있다.
- 때문에 Size를 계산할때 위처럼 계산한다. rear에서 front를 빼고 거기에서 capacity를 더하면,
- 음수이건 양수이건 +가 되고, 이를 capacity로 mod하면 현재의 사이즈가 나온다
- 단, 이렇게 하면, 가득 찼을 때(rear==front)도 마찬가지로 0이 되는데, 이건 어떻게 해결할까?
2) Full = (Rear + 1) % Capacity == Front
- 사실 여러 책들에는 Full을 (Rear + 1) % Capacity == Front로 놓고 계산한다.
- 즉, Rear보다 Front가 한칸 앞에 있으면 (한칸 비워져있으면) 그냥 이걸 가득찬 걸로 보겠다는 것이다.
- 위 그림이 바로 그런 상황이다. 사실 이렇게 계산하면, 위 그림에서 새로운 원소를 못넣는다.
3) 엥...? 굳이 저렇게 까지?
- 그런데, Size를 위처럼 복잡하지 않게 int 변수를 만들어서 넣거나 뺄때 ++, --해서 세도 되고,
- 현재 Front가 Rear보다 더 큰지에 대한 여부를 flag로 주는 방식으로도 손쉽게 구현할 수 있다.
- 사실 지금 위의 낭비가 심하고 복잡한 구현방식(1칸을 빼는것)이 왜 주요 방식이 되었는지 모르겠다.
- 큐 한칸을 뺀다는 것 자체가 너무 큰 낭비이고 (Rear + 1) % Capacity == Front보다는,
- Size == Capacity등의 식이 Full이라는 상태를 표현하는데 있어서 훨씬 직관적이고 간편하다.
- (ps. 왜 위처럼 복잡하게 해야하는지에 대해서 아시는 분 있으면 댓글로 알려주세요 !)
4) Empty = Rear == Front
- 위의 Size와 Full 수식을 사용한다면, Rear와 Front가 같은 위치에 있다면 반드시 Empty이다.
- 모든 원소가 가득 찼을때, 혹은 원소가 한개도 없을 때만 위와같이 Front, Rear가 같은 위치에 있게 된다.
- 만약 Size를 ++, --로 직접세면 Size == 0이라는 매우 직관적인 식이 나온다.
- (아무리 봐도 원형큐는 이렇게 어렵게 구현할 자료구조가 아니다. Size를 직접 세는것을 추천한다)
4. Implementation
1) 한칸 덜 찼을 때 꽉 찬 것으로 간주하는 경우
import java.util.Arrays;
/**
* 1칸 버리는 큐
*/
public class ArrayCircularQueue_1 {
private final int capacity = 5;
private int front = 0, rear = 0;
private int[] array;
public ArrayCircularQueue_1() {
array = new int[capacity];
}
public int size(){
return (capacity + rear - front) % capacity;
}
private boolean isEmpty() {
return front == rear;
}
private boolean isFull() {
return (rear + 1) % capacity == front;
}
public void enqueue(int data) {
if (isFull())
throw new ArrayIndexOutOfBoundsException();
rear = (rear + 1) % capacity;
array[rear] = data;
}
public int dequeue() {
if (isEmpty())
throw new ArrayIndexOutOfBoundsException();
front = (front + 1) % capacity;
int data = array[front];
array[front] = 0;
return data;
}
@Override public String toString() {
return Arrays.toString(array) + " , size : " + size();
}
}
2) Size를 세는 경우
import java.util.Arrays;
/**
* 1칸 안버리는 큐
*/
public class ArrayCircularQueue_3 {
private int[] array;
private int capacity;
private int rear = 0, front = 0;
private int size = 0;
public ArrayCircularQueue_3(int capacity) {
this.capacity = capacity;
this.array = new int[capacity];
}
public ArrayCircularQueue_3() {
this.capacity = 5;
this.array = new int[capacity];
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public boolean isFull() {
return size == capacity;
}
public void enqueue(int data) {
if (isFull())
throw new ArrayIndexOutOfBoundsException();
this.array[rear] = data;
this.rear = (this.rear + 1) % capacity;
size++;
}
public int dequeue() {
if (isEmpty())
throw new ArrayIndexOutOfBoundsException();
int data = this.array[front];
this.array[front] = 0;
this.front = (this.front + 1) % capacity;
size--;
return data;
}
public int peek() {
return this.array[front];
}
@Override public String toString() {
return Arrays.toString(array) + " , size : " + size();
}
}
3) 플래그를 두는 경우
import java.util.Arrays;
/**
* 1칸 안버리는 큐
*/
public class ArrayCircularQueue_2 {
private int[] array;
private int capacity;
private int rear = 0, front = 0;
private char flag = 0;
public ArrayCircularQueue_2(int capacity) {
this.capacity = capacity;
this.array = new int[capacity];
}
public ArrayCircularQueue_2() {
this.capacity = 5;
this.array = new int[capacity];
}
public int size() {
return (capacity * flag + (rear - front));
}
public boolean isFull() {
return size() == capacity;
}
public boolean isEmpty() {
return size() == 0;
}
public void enqueue(int data) {
if (isFull())
throw new ArrayIndexOutOfBoundsException();
this.array[rear] = data;
this.rear = (this.rear + 1) % capacity;
if (front >= rear) flag = 1;
else flag = 0;
}
public int dequeue() {
if (isEmpty())
throw new ArrayIndexOutOfBoundsException();
int data = this.array[front];
this.array[front] = 0;
this.front = (this.front + 1) % capacity;
if (front > rear) flag = 1;
else flag = 0;
return data;
}
public int peek() {
return this.array[front];
}
@Override public String toString() {
return Arrays.toString(array) + " , size : " + size();
}
}
5. Dynamic Array (ArrayList) Circular Queue
- 어레이리스트를 이용하여 크기가 다 찼을 때 grow하면서 원형큐를 구현할 수 있다.
- 주의할 사항이 있는데, grow시 데이터를 옮길 때, front, rear의 위치에 따라 시작점이 중간일 수 있다.
- 때문에 이를 고려해 front부터 rear + capacity까지 루프를 돌려서 front부터 차례대로 담아야하고,
- 기존 배열의 인덱스는 capacity보다 작기 때문에 i % capacity로 mod해서 접근해야한다.
import java.util.Arrays;
public class DynamicArrayCircularQueue {
private int[] array;
private int capacity;
private int rear = 0, front = 0;
private int size = 0;
public DynamicArrayCircularQueue(int capacity) {
this.capacity = capacity;
this.array = new int[capacity];
}
public DynamicArrayCircularQueue() {
this.capacity = 5;
this.array = new int[capacity];
}
public int size() {
return size;
}
public boolean isFull() {
return size() == capacity;
}
public boolean isEmpty() {
return size() == 0;
}
public void enqueue(int data) {
if (isFull())
grow(2.0f);
this.array[rear] = data;
this.rear = (this.rear + 1) % capacity;
size++;
}
public int dequeue() {
if (isEmpty())
throw new ArrayIndexOutOfBoundsException();
int data = this.array[front];
this.array[front] = 0;
this.front = (this.front + 1) % capacity;
size--;
return data;
}
public int peek() {
return this.array[front];
}
private void grow(float rate) {
int newCapacity = (int) (capacity * rate);
int[] newArray = new int[newCapacity];
int newArrayIndex = 0;
for (int i = front; i < rear + capacity; i++) {
newArray[newArrayIndex++] = array[i % capacity];
}
this.front = 0;
this.rear = rear + capacity - 1;
this.capacity = newCapacity;
this.array = newArray;
}
@Override
public String toString() {
return Arrays.toString(array) + " , size : " + size();
}
}
6. List Queue
- 사실 리스트를 쓰면 이렇게 복잡하게 생각할 필요 없이 매우 쉽게 구현할 수 있다. (리스트가 짱이다)
- 노드를 두개를 두는데, Front와 Rear노드를 하나씩 가진다. 이들은 각각 Head와 Tail이다.
- 반대로 Front를 Tail, Rear를 Head로 쓰면, Enqueue할땐 Rear에 노드 하나를 붙이면 되지만,
- Dequeue할때 Front노드에서 하나 떼고 이전으로 돌아가야하는데,
- Singely List는 next 포인터만 가지고 있고, 이전으로 돌아갈수 없기 때문에, Front가 Tail이여서는 안된다.
- Front가 Head일 때는 Front.next를 새로운 Front로 지정하고, 이전노드를 제거(free)하면 깔끔하게 제거되고
- Rear가 Tail일 때는 새로운 노드를 만들고, Tail의 next를 새로운 노드로 연결해주면 된다.
package data_structure.queue;
/**
* @author : Hyunwoong
* @when : 4/29/2020 3:11 PM
* @homepage : https://github.com/gusdnd852
*/
public class ListQueue {
private Node front;
private Node rear;
private int size;
public void enqueue(int data) {
Node node = new Node();
node.data = data;
if (front == null)
front = rear = node;
else{
Node r = rear;
rear = node;
r.next = rear;
}
size++;
}
public int dequeue() {
Node returnNode = front;
front = front.next;
size--;
return returnNode.data;
}
public int size(){
return size;
}
@Override public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("[");
for (Node node = front; node != null; node = node.next) {
builder.append(node.data);
if (node.next != null) {
builder.append(", ");
}
}
builder.append("]");
return builder.toString();
}
private static class Node {
int data;
Node next;
}
}
7. Reference
www.kocw.net
'알고리즘' 카테고리의 다른 글
| 큐 (3) - 덱 (Dequeue) (1) | 2020.04.30 |
|---|---|
| 큐 (1) - 선형 큐 (0) | 2020.04.30 |
| 스택 (2) - 후위 표기법 계산기 (0) | 2020.04.30 |
| 스택 (1) - 개요 (0) | 2020.04.30 |
| 리스트 (3) - 연결리스트 (Linked List) (0) | 2020.04.28 |
| 리스트 (2) - 배열 리스트 (Array List) (0) | 2020.04.28 |
| 리스트 (1) - 개요 (0) | 2020.04.28 |